“Even now, after we’ve been building them for 100 years, it’s very dif-
ficult to understand just why a bicycle works - it’s even difficult to for-
mulate it as a mathematical problem.” — Freeman Dyson interviewed
by Stewart Brand in Wired News, February 1998.
We would like to think that this is the definitive review paper on the linearized equations of the motion for a bicycle:
Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review, Proceedings of the Royal Society A 463:1955-1982. [doi:10.1098/rspa.2007.1857]
J. P. Meijaard, University of Twente, j.p.meijaard@ctw.utwente.nl
Jim M. Papadopoulos, University of Wisconsin-Stout, papadopoulos@alum.mit.edu
Andy Ruina, Cornell University, ruina@cornell.edu
A. L. Schwab, Delft University of Technology, a.l.schwab@tudelft.nl
The paper and supporting material
1) Preprint: 28 page pdf
2) Supporting text, "History of bicycle steer and dynamics studies": 35 page pdf
Introduction
Since their inception bicycles have attracted attention from the more or less wellknown scientists of the day, including thermodynamicist William Rankine, the mathematicians Carlo Bourlet, Paul Appell and Emmanuel Carvallo, the meteorologist Francis Whipple, the mathematical physicist Joseph Boussinesq, and the physicist Arnold Sommerfeld working with mathematician Felix Klein and engineer Fritz Noether (brother of Emmy). A later peak in the ‘single-track vehicle’ dynamics literature began in about 1970, perhaps because digital computers eased integration of the governing equations, because of the increased popularity of large motorcycles (and attendant accidents), and because of an ecology-related bicycle boom. This latter literature includes work by dynamicists such as Neimark, Fufaev, Breakwell and Kane. Starting in the mid-1970s, the literature increasingly deviates from the rigid body treatment that is our present focus.
Whipple, F. J. W. 1899 The stability of the motion of a bicycle. Quart. J. Pure Appl. Math. 30, 312–348. (pdf)
Background
Over the past 140 years, scores of other people have studied bicycle dynamics, either for a dissertation, a hobby or sometimes as part of a life’s work on vehicles. This work started back in the 70's at Cornell University, where Jim Papadopoulos was deriving linearized equations of motion for the Whipple bicycle model (4 rigid bodies with constraints) by hand. Next, together with MSc student Scott Hand checking these results with the vast literature on the equations of motion for a bicycle, they could not find any set which complied with their result. Who was right?
Then in 2002 Arend Schwab from Delft University of Technology was on sabbatical at Cornell, hosted by Andy Ruina. During the fall break he derived linearized equations of motion for the Whipple model with his multibody dynamics software system SPACAR and compared entries in these equations for a generic bicycle with Jim's results. And lo and behold, they complied! To be absolutely sure, Arend asked his longtime friend and colleague Jaap Meijaard, who was at that time at Nottingham UK working on motorcycle dynamics using the Autosim software, to check the result and again they found full agreement with Jim's results!
So what about the vast literature then? The short answer is that only one out of the more than eighty publications we studied was absolutely correct: Dohring 1955. The long answer can be read in the supporting text "History of bicycle steer and dynamics studies" as mentioned above. An annotated version of this history is presented on this page below with comments linked to the references where present.
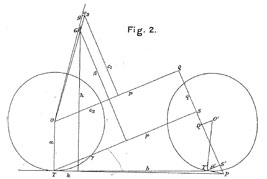
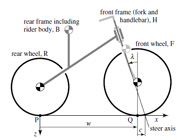
Whipple' s Fig 2: bicycle model
Whipple Bicycle Model
In 1897, French mathematician Carvallo (1899) and then, more generally,
Cambridge undergraduate Whipple (1899) used rigid body dynamics equations to
show in theory what was surely known in practice, that some safety bicycles
could, if moving in the right speed range, balance themselves. Presently, these
same two basic features of bicycle balance are clear:
(i) A controlling rider can balance a forward-moving bicycle by turning the
front wheel in the direction of an undesired lean. This moves the ground contact
points under the rider, just like an inverted broom or stick can be balanced on
an open hand by accelerating the support point in the direction of lean.
(ii) Some uncontrolled bicycles can balance themselves. If an appropriate
typical bicycle is given a push to approximately 6 m sK1, it steadies itself and
then progresses stably until its speed gets too low.The torques for the
self-correcting steer motions can come from various geometric, inertial and
gyroscopic features of the bicycle.
Beyond these two generalities, there is little that has been solidly accepted in
the literature, perhaps owing to the lack of need. Through trial and error
bicycles had evolved by 1890 to be stable enough to survive to the present day
with essentially no modification. Since bicycle design has been based on
tinkering rather than equations, there has been little scrutiny of bicycle
analyses. To better satisfy general curiosity about bicycle balance and perhaps
contribute to the further evolution of bicycle design, we aim here to firmly
settle some basic, and largely previously presented, bicycle stability science.
The core of the paper is a set of easy-to-use and thoroughly checked linearized
dynamics equations for the motion of a somewhat elaborate, yet well-defined
bicycle model.
Implementation
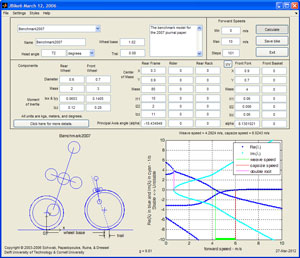
A MATLAB Graphical User Interface (GUI) for the calculation of the stability of a bicycle, the implementation of the linearized equations of motion from this paper, is JBike6, free download here.
- Any questions or
comments? Please contact
Arend L. Schwab
-